Cette semaine, nous donnons la parole à Youen Delalande, étudiant en projet de fin d'études chez TPLM-3D, qui travaille sur la détection des erreurs dans les calculs de réseaux. Il explique :
"La plupart des paramètres inconnus en topographie sont déterminés par des méthodes d'estimation, parmi lesquelles la méthode des moindres carrés est la plus couramment utilisée. Cette méthode donne un résultat optimal lorsque les mesures suivent une distribution normale. Cependant, en pratique, de nombreuses observations ne respectent pas cette distribution, surtout lorsque certaines sont entachées d'erreurs. Pour résoudre ce problème, on peut recourir à des méthodes dites 'robustes' qui ne sont pas sensibles aux erreurs.
Une estimation est qualifiée de robuste lorsqu'elle produit des résultats corrects même en présence d'erreurs grossières dans les observations. L'un des principaux objectifs de ces méthodes robustes est de localiser automatiquement les erreurs dans les mesures. De plus, ces méthodes simplifient l'analyse, le nettoyage et l'évaluation des données, qui deviennent de plus en plus complexes et étendues. Elles permettent également de déterminer les valeurs probables des erreurs, ce qui est très utile pour mieux analyser les résultats d'une compensation et identifier l'origine des erreurs."
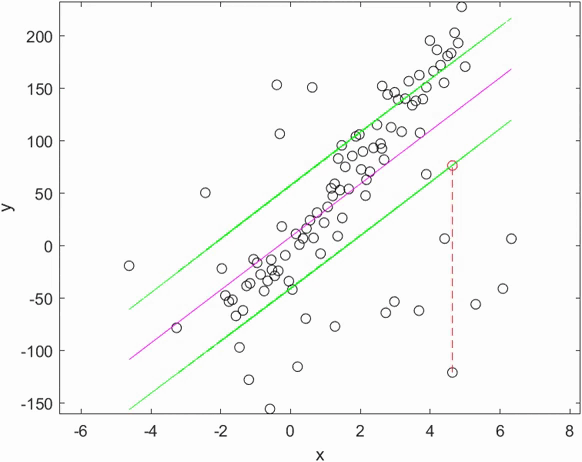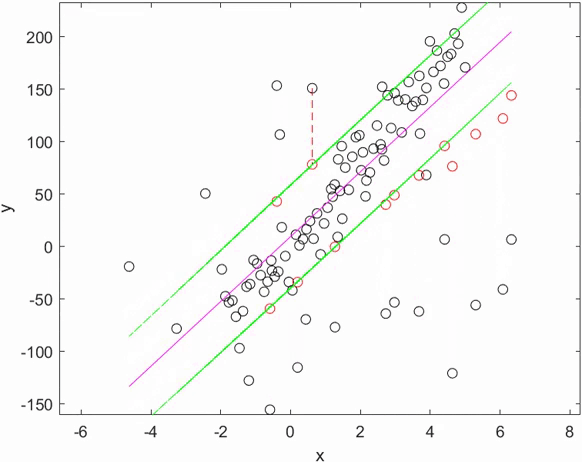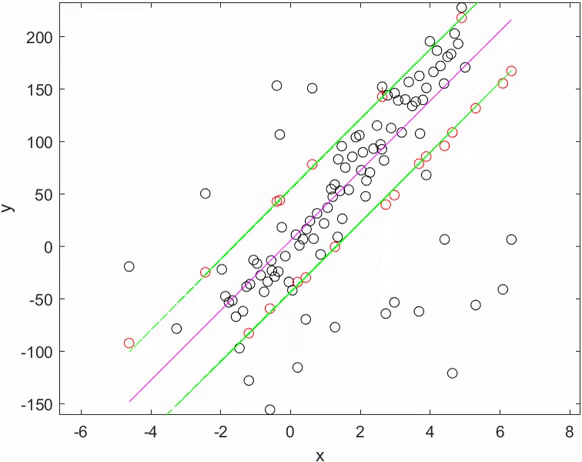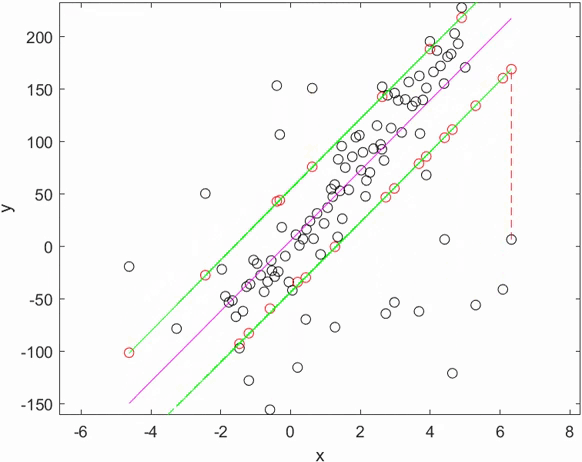
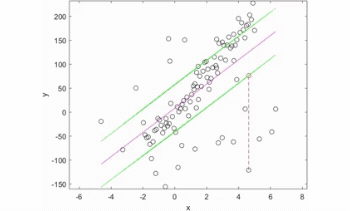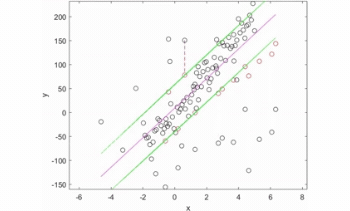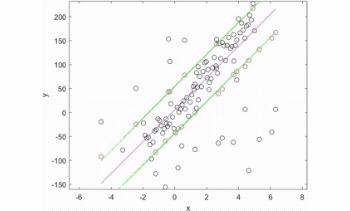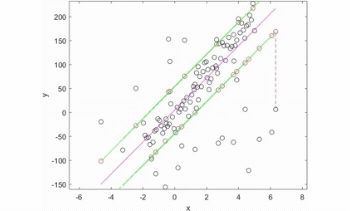
Illustration : fonctionnement d'un estimateur robuste sur une régression linéaire.